Kunwar Abhikeern

Intro

Computational materials researcher specializing in atomistic modeling and data-driven materials discovery. Experienced in molecular dynamics (MD), density functional theory (DFT), and machine learning interatomic potentials (MLIP) for property prediction, phase stability, and mechanism-driven analysis. Expertise in polymerization processes, structure–property relationships, and ML-integrated simulation workflows for advanced materials design.

Education

• Ph.D. in Mechanical Engineering | IIT Bombay (2019-2024)
• M.Tech in Nanotechnology | IIT Roorkee (2015-2017)
• B.Tech in Mechanical Engineering | UPTU (2010-2014)

Hobbies & Interests

• Reading about scientific advancements & space exploration

Contact

Work

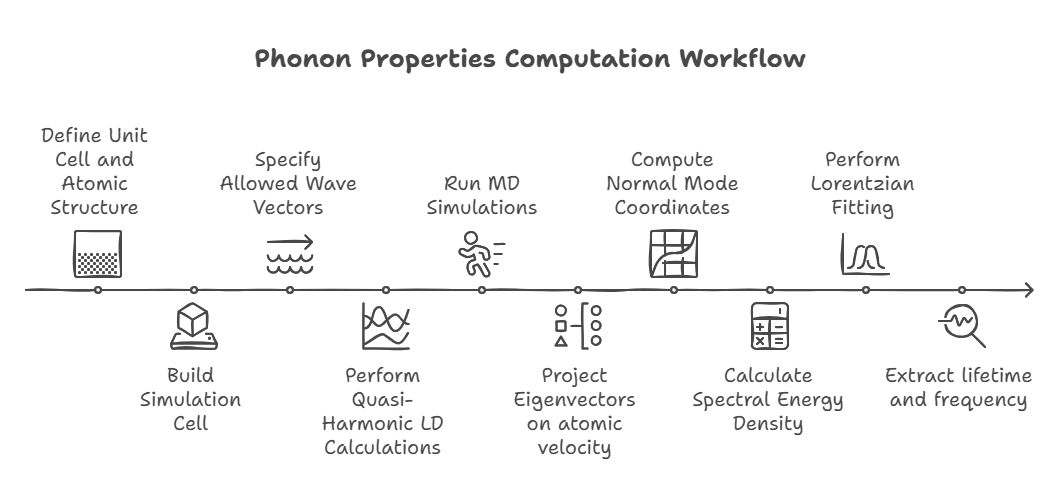
Workflow to get phonon properties

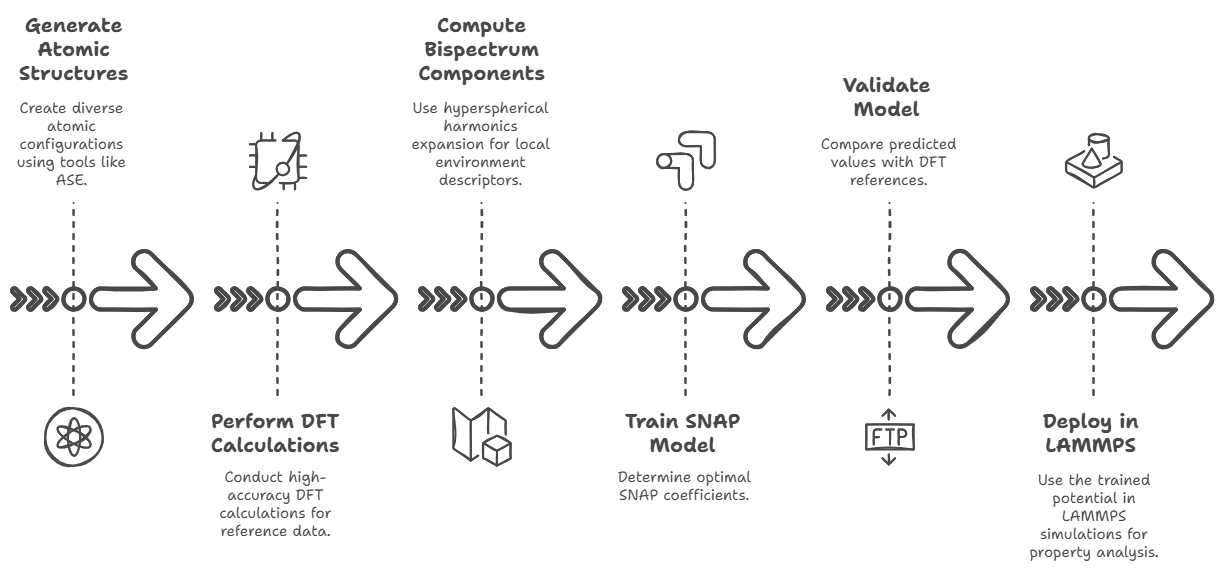
SNAP potential for Mg2Si(x)Sn(1-x)

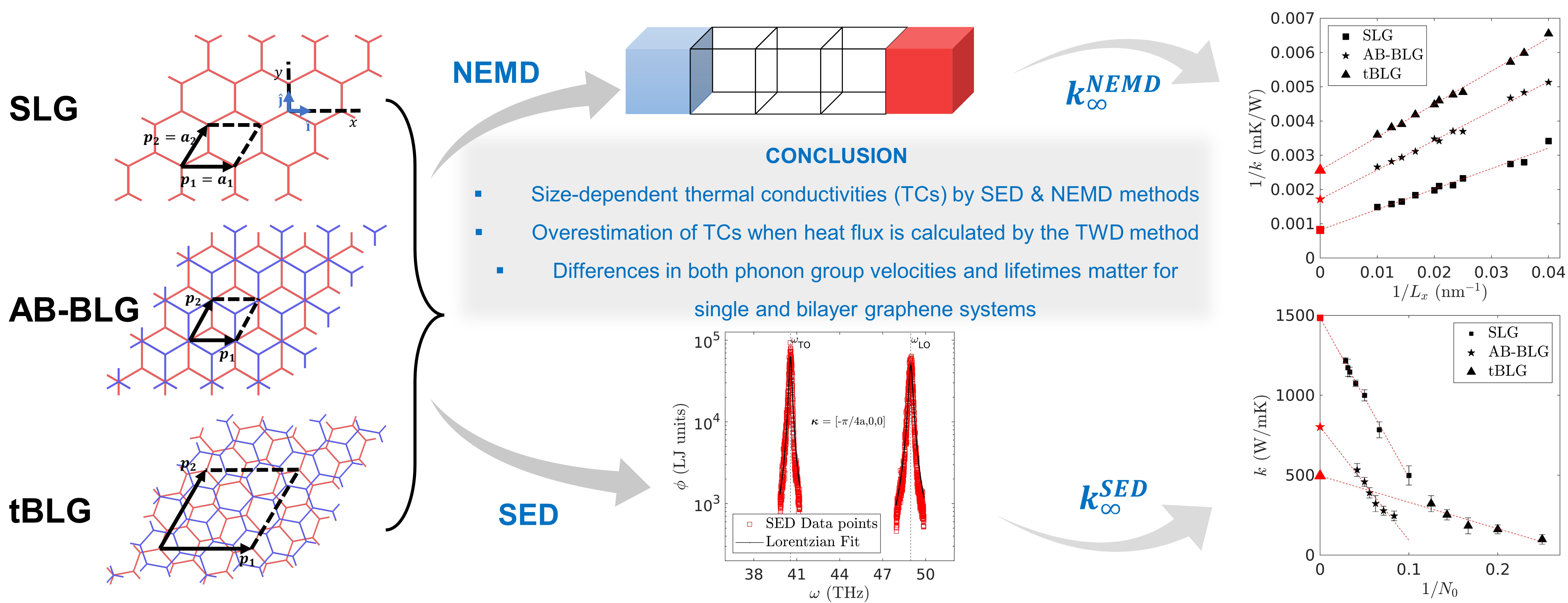
Graphene with layers

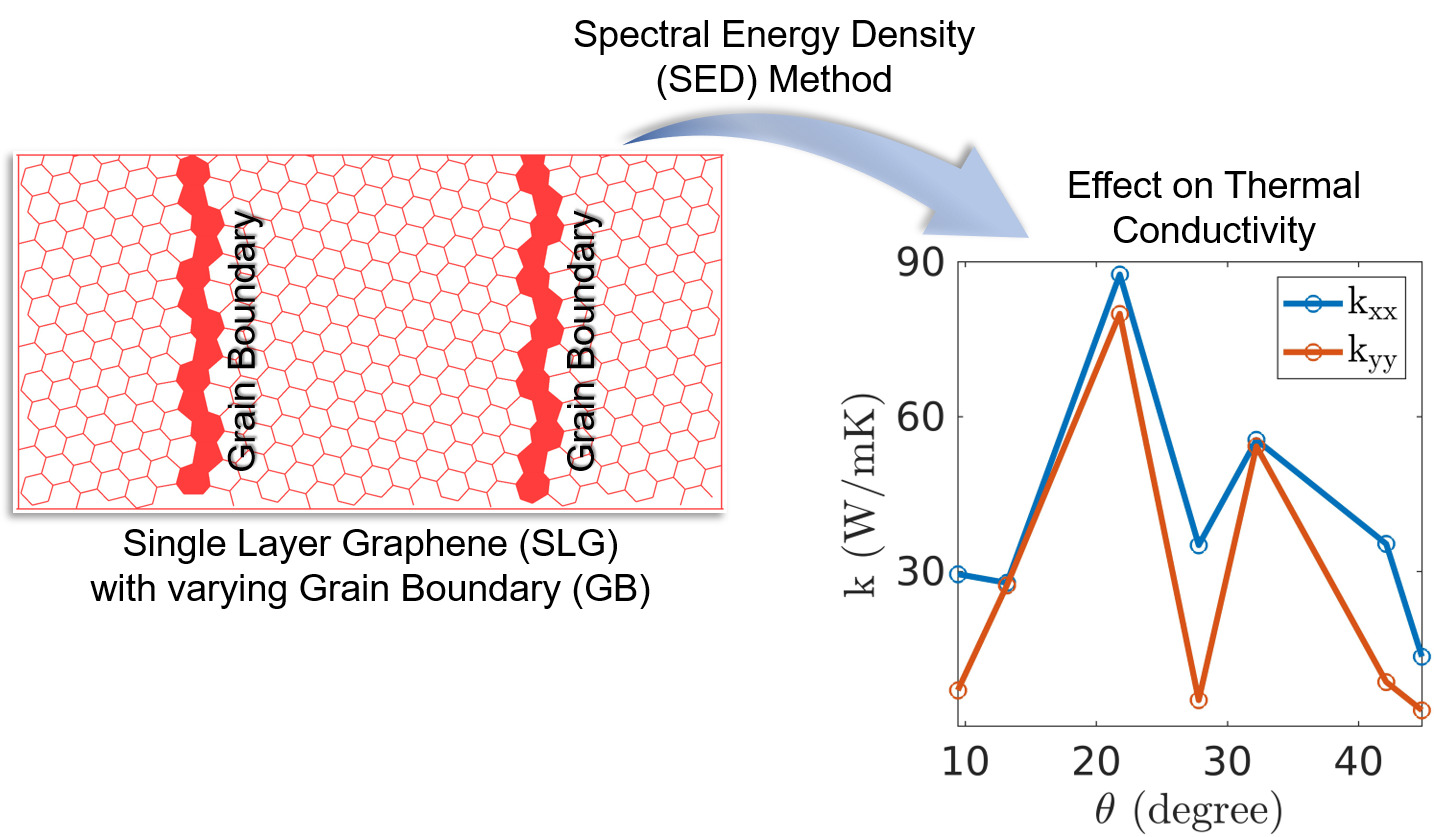
Graphene with grain boundaries

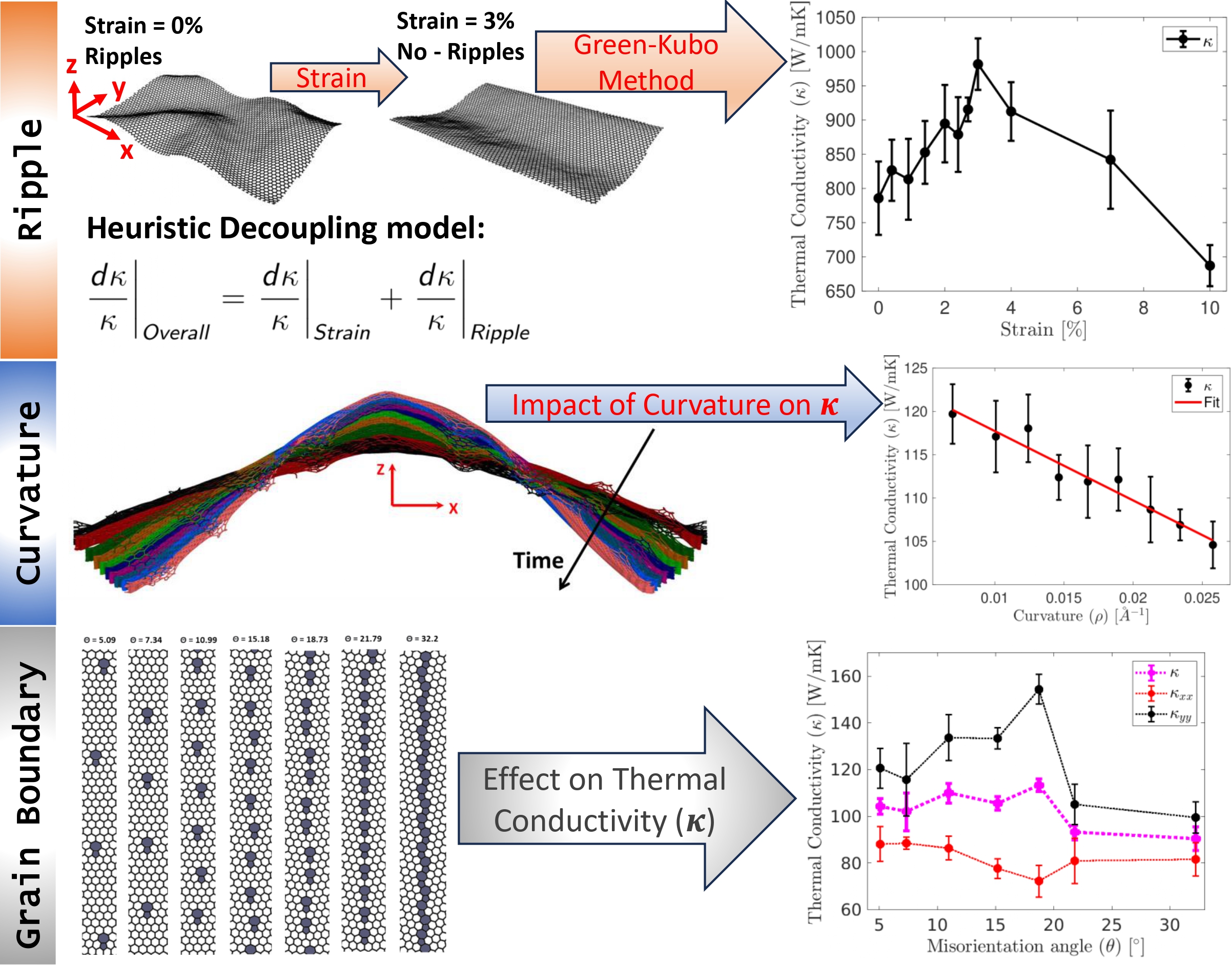
Graphene with strain, ripples, and curvatures

Thesis

Workflow to get
phonon properties

The workflow for computing phonon properties using spectral energy density (SED) analysis begins by defining the unit cell and atomic structure, which is then used to build the simulation cell. Allowed wave vectors \( \mathbf{k} \) are specified before performing quasi-harmonic lattice dynamics (LD) calculations using GULP or Phonopy to obtain wave vectors, frequencies, and mode shapes (eigenvectors). Molecular dynamics (MD) simulations are then run in LAMMPS to generate atomic positions and velocities. The eigenvectors are projected onto atomic positions and velocities to obtain the normal mode coordinates \( \mathbf{q} \), which are then used to compute the spectral energy density \( \phi \). Lorentzian fitting of \( \phi \) extracts the phonon lifetimes \( \tau \) and peak frequencies \( \omega_0 \), along with thermal conductivity \( \kappa \). Since the Boltzmann Transport Equation (BTE) requires \( \tau \), this completes the computational workflow for phonon transport analysis.

SNAP potential for Mg2Si(x)Sn(1-x)

To build a Spectral Neighbor Analysis Potential (SNAP) for a material system like Mg₂Si, one begins by generating a diverse and representative dataset of atomic structures that includes not just the pristine bulk phase but also strained configurations, surfaces, point defects (such as Mg and Si vacancies or interstitials), thermally perturbed snapshots from ab initio molecular dynamics, and possibly doped or alloyed configurations if applicable. These structures are typically created using tools like ASE (Atomic Simulation Environment), pymatgen, or VESTA, and must cover a broad configurational space to ensure that the resulting potential can generalize well. For each of these atomic configurations, high-accuracy quantum mechanical calculations are performed using Density Functional Theory (DFT) with packages such as VASP, Quantum ESPRESSO, or GPAW. The DFT output must include total energies, atomic forces, and stress tensors for every structure. These serve as the reference data for training the SNAP model. Next, the bispectrum components that describe each atom's local environment are computed based on a hyperspherical harmonics expansion, which encodes geometric information into invariant descriptors. This is done using the FitSNAP software, a Python-based interface that works with LAMMPS and is specifically designed for training and applying SNAP potentials. A typical FitSNAP training input includes definitions for elements (Mg and Si in this case), the radial cutoff distance (typically ~5.0 Å), the angular resolution parameter `twojmax` (usually 6–8), and weighting factors for fitting to energy, force, and stress data. Once the bispectrum features are generated, a linear least-squares regression is performed (usually ridge regression with regularization) to determine the optimal SNAP coefficients that minimize the error between predicted and DFT reference values. This results in a trained potential file (`snap-model.snap`) and corresponding parameter file (`snapparam.out`). The quality of the model is then validated on a test set by comparing predicted vs. DFT energy, force, and stress values using metrics such as RMSE. Further validation may involve running LAMMPS simulations (with `pair-style snap`) to compute material properties like phonon spectra (via LAMMPS + Phonopy), elastic constants, or thermal conductivity using equilibrium or non-equilibrium MD. Throughout this process, the key tools include: structure generation software (ASE, pymatgen), DFT codes (VASP, QE), FitSNAP for feature computation and training, and LAMMPS for deployment. Proper data management, hyperparameter tuning (e.g., twojmax, regularization strength), and cross-validation are critical to ensure a robust and transferable potential capable of accurately simulating Mg₂Si under various conditions.

Graphene with Layers

Details about phonon transport in multilayer graphene...

Graphene with Grain Boundaries

Exploration of how grain boundaries affect thermal and electronic properties...

Graphene with Strain, Ripples, and Curvatures

Understanding the impact of mechanical deformations on graphene’s transport properties...

Thesis

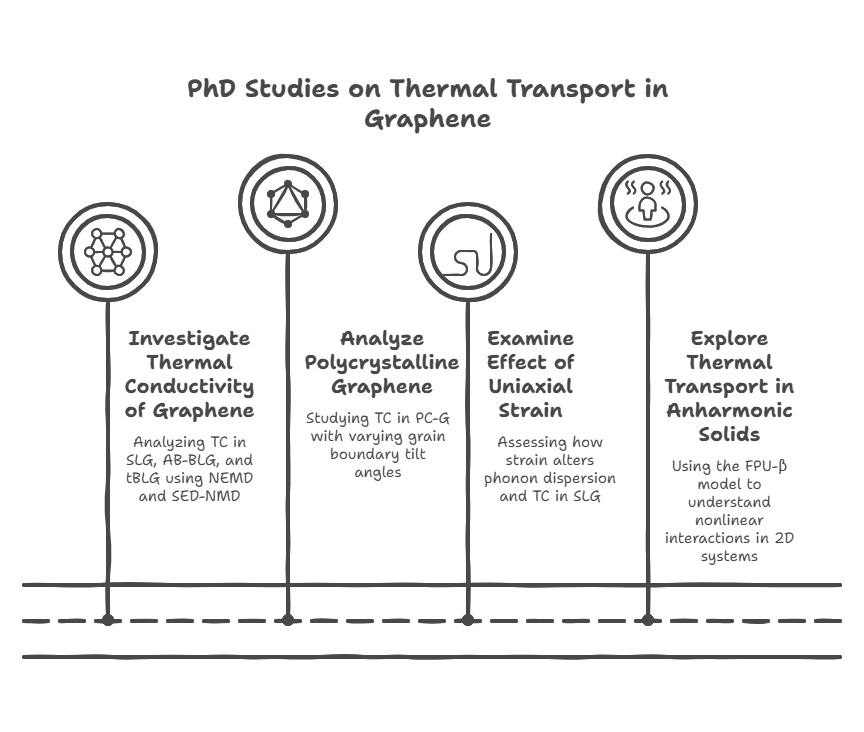
During my PhD, I conducted four key studies to advance the understanding of thermal transport in graphene and 2D materials. First, I investigated the thermal conductivity (TC) of pristine single-layer graphene (SLG), AB-stacked bilayer graphene (AB-BLG), and twisted bilayer graphene (tBLG) using both nonequilibrium molecular dynamics (NEMD) and spectral energy density (SED)-based normal mode decomposition (NMD), revealing that tBLG exhibits lower phonon group velocities and lifetimes, which explains its reduced TC compared to SLG and AB-BLG. Second, I analyzed polycrystalline graphene (PC-G) with various grain boundary tilt angles, demonstrating that TC strongly depends on tilt orientation and is not correlated with phonon density of states or average lifetimes, and I proposed statistical measures to characterize phonon transport based on group velocity and lifetime distributions. Third, I examined the effect of uniaxial strain on SLG and found that strain alters the phonon dispersion—especially the ZA mode—causing a shift from quadratic to linear behavior, and reduces phonon group velocities while leaving lifetimes mostly unchanged, thereby impacting TC. Finally, I explored thermal transport in 2D anharmonic solids using the Fermi–Pasta–Ulam (FPU)-β model for the first time, employing both Green-Kubo and NMD methods to demonstrate the role of nonlinear interactions, with TC showing logarithmic divergence with system size due to size-dependent phonon lifetimes and velocities. Together, these studies offer deep insights into phonon behavior and heat conduction mechanisms in both realistic and idealized 2D systems.

Download CV (PDF)

Download CV (PDF)

Tools

Programming languages: Python, MATLAB, AWK, C++, Bash, HPC Workflows

Simulation software: VASP, Quantum Espresso, LAMMPS, GULP

MLIP frameworks: MACE, DeepMD, Allegro, Magus, M3GNet, OpenCSP

Structure prediction tools: USPEX, XtalOpt

Visualization and analysis: ASE, Pymatgen, phonopy, vasppy, VESTA, Maestro, Ovito, VMD

Soft skills: Communication and team collaboration

Elements

i = 0;

while (!deck.isInOrder()) {
    print 'Iteration ' + i;
    deck.shuffle();
    i++;
}

print 'It took ' + i + ' iterations to sort the deck.';